
Beautiful Spiral Galaxy as seen by the Hubble Space Telescope.
Astronomers and cosmologists today can explain the rotation of disk galaxies such as the Milky Way by assuming that the mass of these galaxies is dominated by an invisible, undetectable dark matter. This arises from simple calculations based on Newtonian gravitation, a 300 year old model that is still used today.
Einstein developed his theory of general relativity about 100 years ago and his GR theory has been shown to be accurate over a wide range of experiments and it certainly is the only widely accepted model of gravitation in use today. There is good reason to rework the simple calculations that lead to the need for dark matter within a GR framework. This has been done now using the latest observational data from the Gaia satellite and has been described by a couple of groups already. Both show that Newtonian gravitation is an incorrect simplification of what gravity is and ignores the fact that gravity is a consequence of rest mass plus a gravitational field, effectively doubling the apparent mass of an object.
This paper describes what we know about gravitation and what we have been getting wrong for many years in applying Newtonian gravitation in place of Einstein’s theory of general relativity. The conclusion simply seems to be that dark matter does not exist within our own galaxies to any significant extent. The apparent mass of galaxies is doubled because of the existence of the gravitational fields of the material within them. This in turn increases the binding energy in galaxy clusters so again making dark matter unnecessary to account for their properties.
Given that dark matter appears to be negligible component of these objects on which we have such good data we should start from the position that dark matter is not a significant component on the largest scales which are important when we look at the formation of large structures in the universe in the earliest times. The consequence of removing the dark matter component from cosmological models will inevitably mean substantial changes and cast doubts on the significance or indeed existence of dark energy as well.
A much more detailed account of what we know of dark matter is included in the paper below:
Does Dark Matter actually exist? June 17, 2024.
Craig Mackay, Institute of Astronomy, University of Cambridge, UK.*
Summary.
Astronomers and cosmologists today can explain the rotation of disk galaxies such as the Milky Way by assuming that the mass of these galaxies is dominated by an invisible, undetectable dark matter. This arises from simple calculations based on Newtonian gravitation, a 300 year old model that is still used today.
Einstein developed his theory of general relativity about 100 years ago and his GR theory has been shown to be accurate over a wide range of experiments and it certainly is the only widely accepted model of gravitation in use today. There is good reason to rework the simple calculations that lead to the need for dark matter within a GR framework. This has been done now using the latest observational data from the Gaia satellite and has been described by a couple of groups already. Both show that Newtonian gravitation is an incorrect simplification of what gravity is and ignores the fact that gravity is a consequence of rest mass plus a gravitational field, effectively doubling the apparent mass of an object.
This paper describes what we know about gravitation and what we have been getting wrong for many years in applying Newtonian gravitation in place of Einstein’s theory of general relativity. The conclusion simply seems to be that dark matter does not exist within our own galaxies to any significant extent. The apparent mass of galaxies is doubled because of the existence of the gravitational fields of the material within them. This in turn increases the binding energy in galaxy clusters so again making dark matter unnecessary to account for their properties.
Given that dark matter appears to be negligible component of these objects on which we have such good data we should start from the position that dark matter is not a significant component on the largest scales which are important when we look at the formation of large structures in the universe in the earliest times. The consequence of removing the dark matter component from cosmological models will inevitably mean substantial changes and cast doubts on the significance or indeed existence of dark energy as well.
Models of Rotating Disk Galaxies.
Dark matter was originally suggsted as one way that the observations of the rotation speeds of disk galaxies could be explained in terms of classical Newtonian dynamics. Astronomers knew that in our solar system planets further from our Sun orbited with velocities which decreased with distance from the sun. When detailed spectroscopic measurements were made of isolated disk galaxies it was expected that that pattern of diminishing rotation speed with distance from the centre of the galaxy would be found. Instead, the rotation curves showed that outside a central core the rotation velocities remained roughly constant with distance from the centre.
The radial brightness profile of a typical disk galaxy declines with distance from the centre. It would only be possible for the rotation velocities to be maintained if the material at any particular point was enhanced by something that we could not detect. Adding in that assumption the rotation curve makes sense within the context of classical Newtonian dynamics but it transfers the problem to one of trying to detect what this missing material might be. This is known as Dark Matter, but despite over 90 years of searching and an incredible amount of theoretical model making to try to account for it, no dark matter has ever been found. What we do know about it is very much what it doesn’t do. It must be able to interact gravitationally with normal (baryonic) matter. However it cannot interact with any radiation because we do not see absorption or emission features in the spectra nor do we see any evidence of any other kind of emission or absorption from it.
Fundamentally we have a hard disagreement between observational studies on one side and basic physics on the other. An extraordinary amount of effort has gone into trying to discover what observational studies should be made. Many extremely expensive instruments have been built, none of which has been successful in detecting dark matter. Great numbers of theoretical astrophysicists have tried to account for this discrepancy but again without success. The discrepancy between observation and the predictions of Newtonian dynamics continues. This note will look at whether it is appropriate that Newtonian dynamics is used in this context.
Is more than 300 years since Isaac Newton set down the 3 laws of motion. They have withstood the test of time very well indeed in many different ways. They apply widely and astronomers certainly expected that they would continue to apply when looking at increasingly great distances as telescope technologies improved. Unfortunately the discrepancies are mounting. A variety of variations of conventional Newtonian dynamics have been examined of which MOND (modified Newtonian dynamics: Milgrom, 1983) is one of the better-known. There are a number of issues with that theory and of course it replaces one unknown (dark matter with its properties) with another that implies changing Newtonian dynamics so that the gravitational forces are slightly increased towards the edge of a galaxy.
The current view is that about 90% of the mass in the universe is dark matter with the other 10% baryonic matter. That is quite remarkable claim for material that has never been detected. The problem has become even more acute recently following exciting results from radio astronomy. If we look beyond the visible edge of a disk galaxy that we see on typical images we find significant quantities of hydrogen. Radio spectroscopy of that hydrogen shows that dynamically it continues the rotation pattern we see in the inner parts of the disk. The dark matter that would be implied by this to maintain the rotation curve we observe would completely dominate the mass of the material at the edges of the galaxy.
We show in Figure 1 examples of the data on two typical disc galaxies.
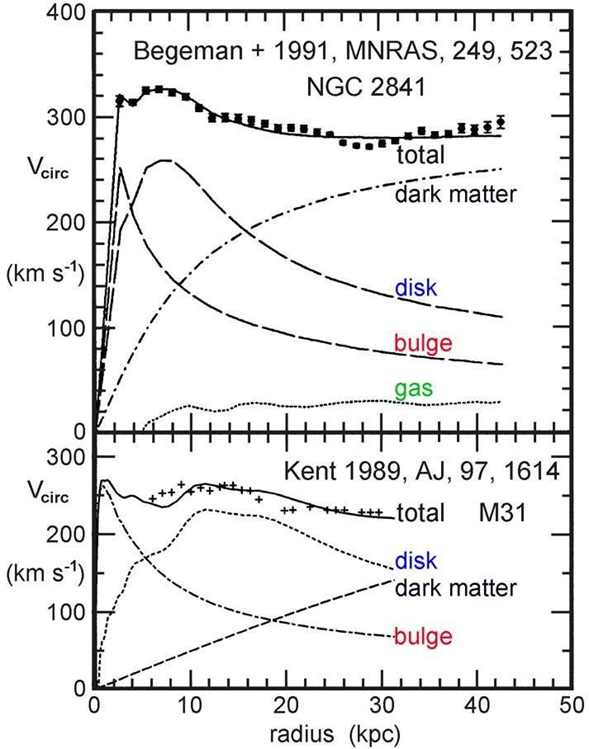
Figure 1: Examples of mass models and rotation curves for individual galaxies. The points with error bars in the upper panels are the observed rotation curves V(R). The errors represent both random errors and systematic uncertainty in the circular velocity due to asymmetry in the velocity field. In both galaxies, the data exceed the lines vbar = √Rgbar representing the baryonic mass models, indicating the need for dark matter. Each baryonic component is represented. The dark matter contribution is assumed to be what should be added to the observed baryonic matter data in order to match the observed total rotation curve.
An important dataset was collated by McGaugh, Lelli and Schombert (2016) who brought together data from 175 nearby disk galaxies which had baryonic mass estimates from good quality 3.6 micron photometry plus high-quality rotation curves from HI/Hα studies. The sample covered very broad ranges of luminosity, surface brightness, rotation velocity and Hubble type. This dataset, known as SPARC (Spitzer Photometry and Accurate Rotation Curves) is currently the largest collection of data on disk galaxies with both high-quality rotation curves and near infrared surface photometry. Great attention was paid to ensuring the data were normalised in as consistent a way as possible so that data from different kinds of observations could be merged. This allows the baryonic Tully-Fisher relation (Tully & Fisher,1977), for example, to be confirmed as a straightforward scaling relation with the baryonic mass proportional to the fourth power of the asymptotic rotation velocity at large radius. We also note that the Tully-Fisher relation derived using total mass estimates for these galaxies (baryonic plus dark matter) has a bigger dispersion than the baryonic Tully-Fisher relation. That observation alone is concerning: adding the derived dark matter to the observed baryonic matter so as to give a poorer estimate of the Tully-Fisher relation is not what one might predict. The tight correlation shown in figure 2 implies that the dark matter if it exists, it must track the distribution of baryonic matter within the disk galaxy to good accuracy and cannot diffuse relative to that baryonic matter significantly. This is a very important new constraint on the properties we must look for in any dark matter candidate.
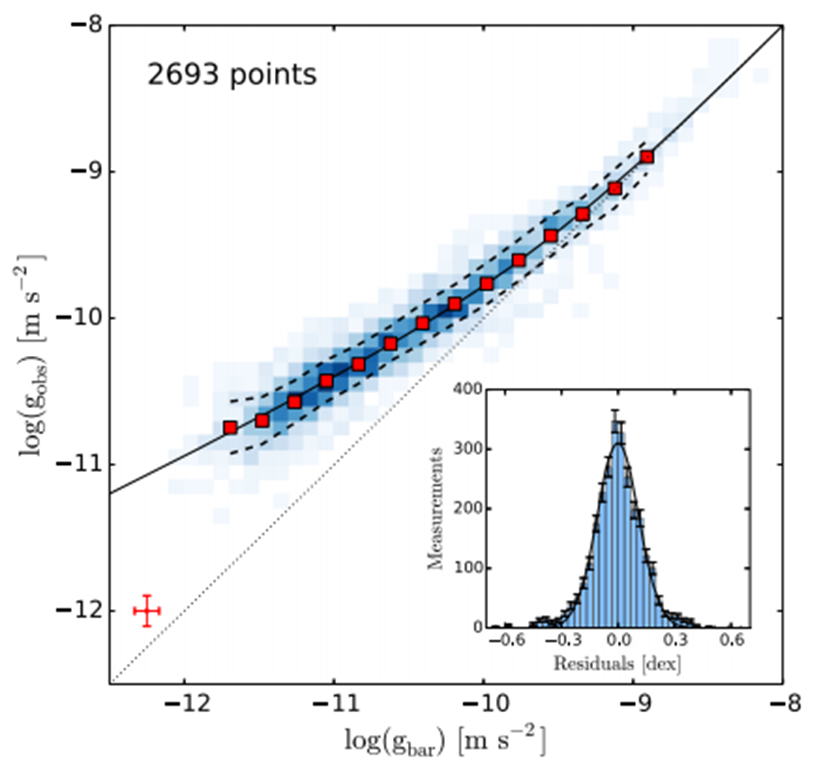
Figure 2 (from McGaugh, Lelli and Schombert (2016)): combines the ~2700 data points from 153 disk galaxies to show the discrepancy between the centripetal acceleration observed in rotation curves for the “observed” mass which includes the added dark matter against the value for the baryonic mass, assumed to be stable. The inset shows the histogram of the residuals around the best fit to the curve.
Most importantly, new results show to a high degree of accuracy, that one can derive the missing mass of a galaxy from its baryonic mass without any other adjustment or correction and without any additional parameters. Whatever dark matter might be it is clearly and unambiguously related to the baryonic matter component of galaxies alone. The derived dark matter content of a disk galaxy may be predicted directly from its baryonic rotation curve without any other physics.
Modelling Stellar Orbits in Disk Galaxies with General Relativity.
We have been very fortunate in the last few years to have access to the extraordinary dataset produced by the Gaia satellite where data on vast numbers of stars in the DR2 data release. It provides parallaxes and proper motions for around 1.3 billion observed objects. Gaia was able to measure radial velocities for about 7 million stars with an effective temperature of between 3550 and 6900 K. The quantity and quality of the data are quite remarkable and have transformed our ability to analyse in detail the dynaics of the stars in the disk of our own galaxy. Two exciting new research papers, Mariateresa Crosta et al (MNRAS 496,2107, 2020) and Davide Astesiano et al (Eur Phys J C 82, 554, 2022) have used the Gaia data to fit to velocity profile rotation curve models, firstly the “traditional” model including a dark matter halo and secondly to a general relativistic model. These papers use somewhat different models of the Milky Way dynamics but both find that the general relativistic approach gives very good fits to the observed data without the need to invoke any significant amount of Dark Matter. They conclude that dark matter is principally a consequence of using Newtonian gravitation models rather than those that are calculated properly using the much more modern general relativity as a gravitational framework.
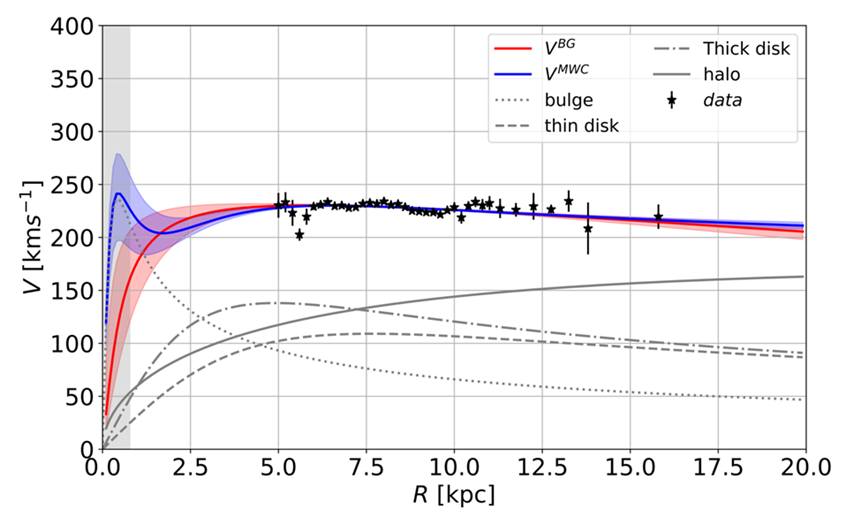
Figure.3. The velocity profile of the Milky Way is derived from a sample of disk tracers selected from the Gaia DR2 dataset. The black starred symbols represent the median values within each as the radial bins. The red and blue curves show the best fit to two different models respectively. The other grey curve represents the kinematic substructures that contribute to typical Milky Way models: the dotted line is for the bulge, dashed and dot-dashed lines offer thin and thick discs respectively and finally the grey solid line illustrates the contribution of the NFW halo. The coloured areas represents the reliability intervals of the fitted curves but note that for radial distances R<5kpc both the classical and relativistic curves are very uncertain because of lack of data in that region. This is taken from Mariateresa et al. (2020). The more recent paper by Astesiano et al (2022) covers a much wider range in R but substantially confirms this result.
The Physics of Newtonian Gravity.
The physics of gravitation as used by astronomers today is substantially that of Newton, published in 1687. Here the gravitational force F between two objects of masses M1 and M2 separated by distance r is given by F = GM1M2/r2 where G is the gravitational constant. Velocities within most astronomical objects such as galaxies or clusters of galaxies are relatively small, much less than the velocity of light, so that special relativistic effects are generally small and so claimed to justify the routine use of classical Newtonian physics, quite incorrectly,
These basic assumptions allow us to deduce the mass of the galaxy given the rotation curve for a disk galaxy simply using Newtonian dynamics. We see the same pattern in our solar system where the mass is strongly concentrated in the centre (the Sun) and the total mass of all the planets is virtually negligible in comparison. Generally, however, we should not expect a pure 1/√r with the more complicated mass distribution in disk galaxies generally, but at least something fairly close to it.
Einstein and General Relativity.
Einstein had laid out the principles of special relativity at the beginning of the 20th century. Many experiments had shown that a range of experiments were unaffected by the motion of the experimental setup relative to a terrestrial reference frame. He showed that the critical physical equations of motion had to be modified so that time as well as space were affected by that relative motion, and that gave basic equations that satisfied observations and are now known as special relativity.
It took Einstein many more years to unscramble what might be happening when gravitation was taken into account. Even Newton appreciated that there was something missing in his own account of the essence of gravity. He said “Gravity must be caused by an agent acting constantly according to certain laws but whether this agent be material or immaterial, I have left to the consideration of my readers.”
Einstein wanted to understand how the observed physics could be maintained if the frame of reference was falling under gravity. He came to the conclusion that the Newtonian view which was that the source of gravity is simply the rest-mass of an object was not adequate. He believed that we must understand that the source of gravity should be understood as being the rest mass plus the gravitational field. Indeed Einstein had initially predicted the deflection of rays of starlight as they passed the sun. By including the effect of the gravitational field Einstein effectively doubled that deflection from his previous calculations that were simply from Newtonian physics. The data taken during the eclipse of 1919 verified the updated calculation and sealed the reputation of Einstein at that time.
Unfortunately Einstein’s understanding that gravitational fields themselves have energy-momentum has been widely ignored by cosmologists and those trying to understand the apparent imbalance in the internal dynamics of disk galaxies. A gravitational field has energy-momentum which is ignored with Newtonian dynamics. Lynden-Bell & Katz(1985) have shown that mass energy in relativity in a specific instance actually contains twice the classical gravitational potential energy. This is the reason that the gravitational lensing equation gives twice the deflection of the classical calculation. More generally, the presence of a gravitational field can lead to a nonlinearity whose origin can ultimately be traced back to gravitational field self-interaction.
Understanding the Internal Dynamics of Disk Galaxies
The mathematics that physicists use when dealing with general relativity are complicated. When dealing with simple Newtonian dynamics the calculations are relatively straightforward involving position, energy and momentum. In general relativity, however, there are more complicated terms that cannot be ignored. The motion of an object in GR can be very complicated and depends on the way that the stress-energy tensor interacts with its environment.
The approach to using mathematics to understand GR is usually based on a gravitoelectromagnetic approach (Astesiano & Ruggiero, 2022). There are two solutions to these field equations. Firstly when there is a mass current, GR effects become vanishingly small as the mass current itself (the movement of mass into or out from the volume being considered) becomes negligible. This comes directly from the non-homogeneous solution. There is another solution when there is no mass current at all. In galaxies like our own the velocities are very small compared to that of light. Einstein, Infeld & Hoffman, (1938) showed that if we have two masses, M1 and M2 separated by a distance r then the Lagrangian has non-Newtonian potential terms of the form G2M1M2(M1 + M2)/2r2, even at first order and where G is the gravitational constant. This term is independent of any velocity and becomes important whenever large masses are involved. This leads to the homogeneous solution, often ignored by cosmologists and it is here that the GR effects can be really quite substantial and certainly cannot be ignored.
We can understand why this is plausible just by thinking about the forces that a star like our own Sun experiences. Astronomers generally use Newtonian physics which assumes there is a force that attracts the star to the rest of the galaxy. That is equivalent to assuming the galaxy can be represented as a single mass at its centre. That assumption is equivalent to assuming the stress energy tensor is very simple. Under general relativity a number of things are different. Firstly our Sun is also attracted to all the other masses in our galaxy and we now know that we must include the forces of attraction that are the combination of the force of gravity from the rest masses as well as the gravitational fields from all the other objects. We must not imagine that this gravitational field is some kind of nebulous structure. It has energy and that energy is equivalent to a certain amount of mass according to Einstein’s famous equation, E = mc2. There are other forces working as well where gravitational fields can arise from rotating structures due to the Lense-Thirring effect. The net effect is that our Sun is much more strongly influenced by the rest of our galaxy and affected by much more complex forces than might be imagined from simple Newtonian dynamics. That is critical because the whole concept of dark matter is designed to provide that an additional gravitational attraction by assuming there is additional mass wherever rest-mass occurs. Modelling using GR means that we do not need to use as much dark matter if indeed any.
The Physics of Gravity In General Relativity.
It was Einstein who realised what was the true source of gravity and had to include the gravitational field. Newtonian dynamics understands gravity as being due simply to the rest mass of a material object. Einstein realised that gravity is a consequence of the rest mass of an object plus the energy-momentum of the gravitational field. It is that additional component that is ignored by most cosmologists today. In our own solar system the mass is strongly concentrated in the centre (the Sun) and the total mass of all the planets is virtually negligible in comparison. Astronomers did not expect perfect 1/√r to define the rotation velocity at a distance r, but certainly very close to that. However the conclusion from figure 2 is simply that the rotation curve for a disk galaxy allows us to deduce the mass of a galaxy using Newtonian dynamics without any other parameters.
The rotation curve that we observe generally for these galaxies is much closer to being flat (constant velocity with radius) well outside the central core and that is the problem we are trying to understand. The simplest way these observations could be understood within the Newtonian framework was that there had to be invisible mass in these galaxies which would increase the local theoretical rotation velocity to explain the observations they had made.
The full Lagrangian completely constrains the way a star can move. Originally just a reformulation of classical mechanics introduced by Lagrange in 1788, it has since been further reformulated in special, general relativity and more generally in field theory.
A gravitational field has energy-momentum which is ignored within Newtonian dynamics. This was understood by Einstein who recalculated the gravitational lensing equation that predicted the deflection of light passing close to the edge of the Sun. He found that a calculation including GR gave twice the deflection of the classical, Newtonian, calculation. More generally, the presence of a gravitational field can lead to a nonlinearity whose origin can ultimately be traced back to gravitational field self-interaction often called frame-dragging. Very simply this says that all the matter in a galaxy is attracted to all the other matter in the galaxy so the net forces and fields are much more complex and have to be studied with the appropriate mathematics, the mathematics of GR.
Most branches of physics have been refined substantially in the last 300 years and it is important that we look carefully at the assumptions that go into our current use of Newtonian physics for gravitation, particularly as cosmologists often assert they are using general relativity anyway in their mathematics. That is true but then they make assumptions that are equivalent to eliminating GR effects completely from the equations.
Most galaxies and clusters of galaxies are clearly inhomogeneous and far from uniform. The additional terms that give rise to the nonlinearity or field self-interaction start to become important when masses and sizes become very large. This is certainly the case with galactic masses and scales so this must be an important aspect of gravitational forces in such objects. Even on a much smaller scale, these effects are observable when we look at the precession of the orbit of the planet Mercury around our Sun. Only with GR can it be properly accounted for.
The conclusion from these theoretical studies is that the gravitational binding of massive objects, galaxies and clusters etc, may be significantly different from the Newtonian predictions for objects that are not spherically symmetric due to very important higher-order effects.
Although this behaviour may seem strange it should not surprise us. What has been ignored historically is that gravity is a field. We are familiar with fields in electromagnetism. The physics of these fields tells us that in electromagnetism the field dictates how charged particles move and how these charged particles in turn generate the field when they move. There is nothing special about gravity. It is simply another field, the field determining how particles with mass move and how those moving particles in turn generate gravitational fields.
Calculating the forces experienced within and outside a complex object like a galaxy is far from easy. Fortunately Einstein has shown astronomers already familiar with gravitational lensing that Newtonian calculations must be corrected to allow an accurate prediction of the deflection of light around the sun. Einstein’s new prediction was confirmed by Eddington in 1919. We also know that the velocity of propagation of gravitational events is the speed of light as demonstrated during the recent gravitational wave detection of GW170817 at optical wavelengths (Abbott et al, 2017) . In other words, in particle language, photons and gravitons (the elementary particles that are responsible for the gravitational field) travel along the same geodesics, and at the speed of light, c.
Do We Need Dark Matter at All?
What we have found is that within the context of GR any particle of matter within the galaxy is bound to it more substantially than had been assumed under Newtonian dynamics. Essentially we are saying that the mass-energy of a galaxy is considerably bigger than it had been assumed to be when we neglected the gravitational field and assumed there was only the baryonic rest mass holding it together with the help of dark matter.
Building a cluster of galaxies becomes much easier if the individual galaxies have a larger mass-energy than had been assumed. There is much less reason to expect a significant contribution from dark matter to the binding energy of a cluster of galaxies.
More widely, it is becoming clear that we need to recalculate almost every stage of the formation and evolution of our universe. Including the mass-energy of gravitational fields from the earliest stage of the evolution of the universe inevitably will change almost every aspect of the way it evolves. The small changes in the expansion rate that are currently attributed to dark energy may or may not survive these re-calculations and that will undoubtedly change or perhaps eliminate the need for dark energy in our cosmology.
Conclusions.
It is nearly 100 years since the idea of dark matter was introduced once it was found that the internal dynamics of disk galaxies could not be explained satisfactorily on the basis of standard Newtonian dynamics which worked well for the orbits of the major planets in our own solar system.
Einstein produced his theory of general relativity over a hundred years ago and that has been demonstrated on many occasions to be an essential component in understanding gravitational dynamics in many different circumstances. The precision timing required for the GPS satellite system requires the equations of GR to be included and without which accurate terrestrial navigation would be impossible. Understanding the orbital dynamics of the double pulsar required an understanding of GR and within our own solar system the explanation of the precession of the perihelion of the planet Mercury in our own solar system requires the inclusion of the appropriate GR terms.
We should not, therefore, be surprised that an understanding of the internal dynamics of a galaxy such as the Milky Way might depend on GR as well. The calculations are complicated and the mathematics challenging but we now have data in sufficient quantity and of the highest quality from the Gaia astrometric satellite that allow those mathematics to be done correctly. The conclusion from those trials described above is that there is no need for dark matter in any significant quantity to explain the dynamics of the Milky Way.
Indeed, it is difficult to see how important it is otherwise for astronomers to include dark matter in other astronomical theories including those used to understand the formation and evolution of large structures in the universe or the internal dynamics of clusters of galaxies. Until these are recalculated without adding this still-invisible, still-undetected material that is known as dark matter. It seems highly likely that the 90% of mass of the universe attributed to dark matter is simply not be there at all. Back to the drawing board.
Acknowledgements.
The author is grateful for helpful discussions with a number of colleagues in the Institute of Astronomy and Kavli Institute for Cosmology Cambridge. The author is grateful to the University of Cambridge for supporting this work under a VRA contract.
References
Abbott, Benjamin P., et al. “GW170817: observation of gravitational waves from a binary neutron star inspiral.” Physical review letters 119.16 (2017): 161101.
Astesiano, D. et al, (2022) Eur Phys J C 82, 554.
Astesiano, D. and Ruggiero, M. L. (2022) Phy Rev Lett, 106,L121501.
Einstein, A., Infeld, L., & Hoffmann, B. (1938), Annals of Mathematics, 39, 65.
Lynden-Bell & Katz, J.,(1985) MNRAS 213,21-25.
Mariateresa Crosta et al, (2020) MNRAS 496,2107.
McGaugh, S. S., Lelli, F., & Schombert, J. M. (2016), Phys.Rev. Lett., 117, 201101.
Milgrom, M. (1983), Astrophysical Journal, 270, 365,
R.B. Tully, J.R. Fisher, (1977) A&A 54, 661
Zee, “Einstein Gravity in a Nutshell” (Princeton University Press, Princeton, 2013).
Ultimate Social Media – Define which pictures & texts will get shared
Toggle panel: Ultimate Social Media – Define which pictures & texts will get sharedOpen document settingsOpen publish panel
- Post
